Increased, measured mass accuracy and resolution is now a dominant tool for structural characterization in various applications beyond early drug discovery. With their broad reach of specificity and utility, quadrupole time-of-flight (QTOF) instruments, offered by a number of manufacturers today, are replacing other LCMS technologies.
Even though higher order instruments exist, a QTOF instrument’s high mass accuracy falls within a few parts per million of the true, calculated, monoisotopic value, and its high resolution—as much as 10 times higher than a quadrupole instrument’s—permits us to determine empirical formulas according to mass defect (where the critical mass value of hydrogen and other atoms present serve as a differentiator). Speciation analysis—discerning the difference between an aldehyde and a sulphide, for example—becomes possible with an increase in mass accuracy above the quadrupole limits to 30 ppm, where the two masses differ by 0.035 Da. Differentiation between the metabolic processes involving methylation is more demanding, however. Adding CH2 produces an increase over the precursor (response for the drug alone) in the measured mass of +14.0157 Da, as compared with a two-stage biotransformation involving hydroxylation (addition of oxygen) followed by oxidation at a double bond (loss of H2), which produces an increase of +13.9792 Da. Yet both measurements, when limited by nominal resolution—a typical quadrupole response—will look like +14 Da.
Low resolution quadrupole instruments perform well for extremely high mass-accuracy measurements, like those used for analyzing proteins. The masses of proteins are generally defined as “average” values when the isotope peaks are not resolved relative to each other. Average mass is the weighted mean of all the isotopic species in a molecule. The instrumental resolution normally employed on quadrupole instruments broadens the resolved response for a 10 kDa protein by a factor of x1.27. That factor increases significantly as the mass increases (for example, to x2.65 at 100 kDa). However, by reducing the peak width to m/z 0.25 (increasing resolution to 4000 resolution) rather than limiting the instrument resolution to 1000 using the typical peak width (m/z 0.6) improves the situation dramatically.
In practice, ESI-MS analyses of large molecules produce multiply charged ions. Hence the widths need to be divided by the number of charges on an ion to give the width on the mass-to-charge ratio scale. For example, a 20 kDa protein with 10 or 20 charges on it will produce isotope envelopes that are 0.9 or 0.45 m/z units wide at m/z ~2000 or ~1000 respectively.
When these ions are observed on an instrument set for a significantly lower resolution than that required to resolve the isotopes (say less than 10,000 resolution), a single peak is produced for each charge state. The overall width is determined by combining the instrument peak width with the theoretical width of the isotopic envelope divided by the number of charges on the ion. The instrumental peak width would be determined on the first isotope peak of a low-molecular-weight compound at the same m/z value as the multiply charged protein peak.
Consider the requirements for unambiguous characterization from the Journal of the American Society for Mass Spectrometry author’s guidelines (March 2004). For C, H, O, N compositions (C0-100, H3-74, O0-4 and N0-4) a nominal mass-to-charge response at 118 needs only an error not exceeding 34 ppm to be unambiguous, where a m/z response at 750 requires precision better than 0.018 ppm to eliminate “all extraneous possibilities.”
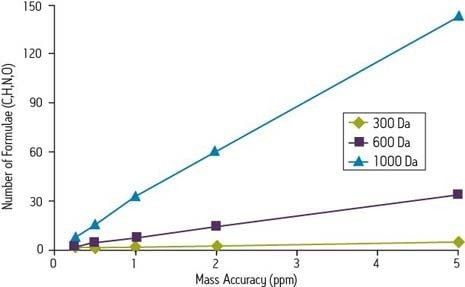

According to the Accurate Mass Best Practice Guide of the VIMMS Programme, an initiative that forms part of the UK National Measurement System, most instruments used for accurate mass measurements are capable of achieving precision of 10 ppm or better.
A calculated mass of 118 Da measured by a modern mass spectrometer to within 2 mmu accuracy would display 17 ppm error, sufficient by today’s standards for unambiguous determination of a chemical formula of that mass:
Monoisotopic calculated exact mass = 118 Da
Measured accurate mass = 118.002 Da
Difference = 0.002 mmu
Error [Difference/exact mass x 106] = 17 ppm
An instrument capable of a response at 750 m/z, also deficient by 2 mmu, would be accurate to 2.7 ppm. In the first case, the measurement is more than sufficient for unambiguous identification of a chemical formula, according to the published standards of the Journal of The American Society for Mass Spectrometry. But in the latter case, the measurement is insufficiently precise. Only the highest order Fourier transform ion cyclotron resonance mass spectrometry (FTICR) can achieve such precision at higher masses.
A comprehensive method of evaluating instrument mass accuracy measurement capability which resembles intended use is by calculating the root mean square or RMS error. To illustrate its use, the following is adapted from the mass measurement accuracy specification of a commercial TOF mass spectrometer.
"The mass measurement accuracy of the instrument, under normal operating conditions, will be better than a given ppm RMS over the given m/z range, based on a number of consecutive repeat measurements of an analyte peak (of given m/z), using a suitable reference peak (of given m/z). Analyte and reference peaks must have sufficient intensity and be free of interference from other masses."
There are some important points and assumptions need to be considered:
The RMS error is calculated using the following relation, where Eppm is the ppm error, and n is the number of masses considered:
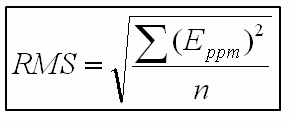
It is worth noting the RMS error allows some measurements to fall outside the ppm error “window of interest” (e.g., 5 ppm RMS). To ensure quality measurements, the conditions described above need to be satisfied (particularly regarding intensity and influence of interferences - balanced ion statistics with clear peak definition in the spectra) over a number of repeat injections. Many reported resolution and mass accuracy numbers that you see are not RMS error numbers but instead originate from a single selected (favorable) ion.
It is important to remember in all applications that a weak signal (excessively high resolution) can yield poor ion statistics and can therefore be unusable. Too strong a signal can be equally useless, causing detector saturation. Ideally balanced ion statistics with definition in the spectra is the goal.
Some comparisons with respect to the figure:
It is important to appreciate the various inter-related roles played in accurate-mass precision by the shift between definitions of mass and increasing resolution and factors such as peak shape and the need for calibration. If these are not clearly understood and taken into consideration mass mis-assignments and other undesirable results may occur.
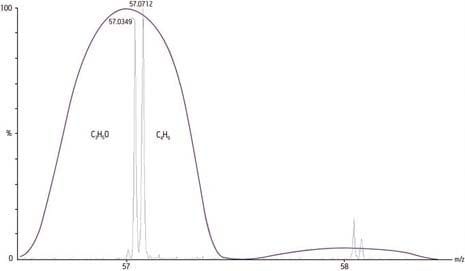
The two fragments of different compositions in the figure are from the same analyte and therefore in the source at the same time. Even the best chromatography won't help in this case so this emphasizes one of the reasons higher resolution is useful especially in the analysis of unknowns. This applies equally well to QTof product ion data versus product ion data from a triple quad. As an added advantage with this higher degree of resolution the extracted ion current (XIC) plot of each allows differentiation of the oxygen containing and alkyl containing analytes selectively from the chromatograms where the quad data would lack this capability.
See MS – The Practical Art, LCGC
Also:
Sulphamethazine Nominal = 278
[C12H14N4O2S]
Average mass – Calculated using all isotopes of each element and their natural abundance.
Sulphamethazine avg. mass = 278.3313
[C12H14N4O2S]
Calculated exact mass – (Monoisotopic). Determined by summing the masses of the individual isotopes for a given ion.
Sulphamethazine exact mass = 278.0837
[C12H14N4O2S]
Accurate mass – (Actually “measured exact mass”). What we do with our instruments. It is the measure of an m/z reported to (typically) three or four decimal places.
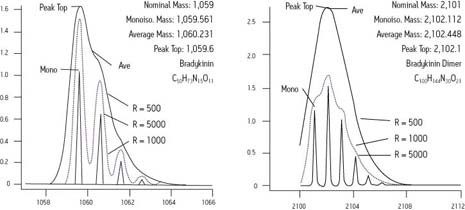
As mass increases, differences between the definitions increase, and peak shape plays a bigger role:
Ubiquitin Nominal Exact Average
[C378H630N105O118S] 8556 8560.6254 8565.8730
Understanding Mass Spectrometry
What is MS and How does it Work?
Biomolecular Ionization Methods
What Types of Instruments Are Used?
Mass Accuracy and Resolution
Interpreting Mass Spectrometer Output
Solvents and Caveats for LC-MS
FAQs about Mass Spectrometry
What is mass accuracy?
Mass accuracy is the measure of how close the measured mass of an ion is to its true mass.
What is mass resolution?
Mass resolution is the ability of a mass spectrometer to distinguish between two ions of similar mass.
How is mass accuracy measured?
Mass accuracy is measured by comparing the measured mass of an ion to its true mass.
How does mass resolution affect the accuracy of a mass spectrometer?
Mass resolution affects the accuracy of a mass spectrometer by allowing it to distinguish between two ions of similar mass.
What is the difference between mass accuracy and mass resolution?
Mass accuracy is the measure of how close the measured mass of an ion is to its true mass, while mass resolution is the ability of a mass spectrometer to distinguish between two ions of similar mass.